class 10 chapter 12 (area related to circles) class notes

 

CBSE Class 10 Maths Notes Chapter 12 Areas related to Circles

Circumference of a circle = 2πr
Area of a circle = πr² …[where r is the radius of a circle]
Area of a semi-circle = πr22
Area of a circular path or ring:

Let ‘R’ and ‘r’ he radii of two circles
Then area of shaded part = πR² – πr² = π(R² – r²) = π(R + r)(R – r)

Minor arc and Major Arc: An arc length is called a major arc if the arc length enclosed by the two radii is greater than a semi-circle.

If the arc subtends angle ‘θ’ at the centre, then the
Length of minor arc = θ360×2πr=θ180×πr
Length of major arc = (360−θ360)×2πr

Sector of a Circle and its Area
A region of a circle is enclosed by any two radii and the arc intercepted between two radii is called the sector of a circle.
(i) A sector is called a minor sector if the minor arc of the circle is part of its boundary.
OAB^ is minor sector.

Area of minor sector = θ360(πr2)
Perimeter of minor sector = 2r+θ360(2πr)

(ii) A sector is called a major sector if the major arc of the circle is part of its boundary.
OACB^ is major sector
Area of major sector = (360−θ360)(πr2)
Perimeter of major sector = 2r+(360−θ360)(2πr)

Minor Segment: The region enclosed by an arc and a chord is called a segment of the circle. The region enclosed by the chord PQ & minor arc PRQ is called the minor segment.

Area of Minor segment = Area of the corresponding sector – Area of the corresponding triangle

Major Segment: The region enclosed by the chord PQ & major arc PSQ is called the major segment.
Area of major segment = Area of a circle – Area of the minor segment
Area of major sector + Area of triangle

cbse class 10th areas realated to cirlces

Share:

Read More

Class 10 chapter 11 (CONSTRUCTIONS) class notes

 

Notes on Constructions

Division of a Line Segment

If we have to divide a line segment in particular ratio, then we can do it by measuring the length on the ruler and mark it on the line. But if we don’t have anything to measure then we can do it by using steps of construction.

Method 1

 AB is a line segment of 4 cm. Divide it in the ratio of 1:3 using a compass.
Steps of Construction
Step 1: Draw a line AC of any length by making an acute angle with the given line segment AB.
Step 2: Using any small length on the compass mark 4 points of equal size on AC, so that AX₁ = AX₂ = AX₃ = AX₄.We are marking 4 points as we have to divide the line in the ratio of 1:3, so 1 + 3 = 4.
Step 3: Now join BX₄.
Step 4: Draw a line from point X₁ to line AB parallel to BX₄, which intersects AB at point P.
Now AP: PB = 1:3.

Method 2(Alternative Method)

A line can also be divided by another method.
Steps of Construction
Step 1: Draw a line AC with the acute angle with the line segment AB.
Step 2: Draw another line DB parallel to AC so that ∠BAX = ∠ADB

Step 3: Mark the points X₁(m = 1) on AC and Y₁, Y₂, Y₃ n = 3) on DB so that AX₁ = BY₁ = Y₁Y₂ = Y₂Y₃.

Step 4: Join X₁Y₃ so that it intersects line AB at P.

AP:PB = 1:3

Construction of a Triangle similar to a given Triangle as per given Scale

The scale factor is the ratio of the sides of the triangle given to the sides of the triangle to be made by the steps of construction.

Example:

Draw a triangle similar to ∆ABC with its sides equal to 2/3 of the corresponding sides of the given triangle ABC. (Scale factor = 2/3).

Steps of Construction

Step 1: Draw a line AX by making an acute angle with the line segment AB.

Step 2: Mark three points of equal size using a compass on the line AX. Points will be depending upon the scale factor as we have to mark the number of points which is greater in the scale factor. In the ratio of 2/3(3 > 2).

Step 3: Join BX₃ and draw a line from X₂ parallel to BX₃ to intersect AB at P.

Step 4: Draw a line parallel to BC from point P to intersect AC at Q.

Now ∆APQ ~ ∆ABC.

Remark: Here we have made a similar triangle which is smaller than the given triangle because the scale factor was 2/3. But if we have scale factor like 5/3 then we will make a bigger triangle then the given triangle by taking 5 points on the line).

Construction of Tangents to a Circle

Tangent is a line which intersects the circle at one point only at the outer of the circle. It is always perpendicular to the radius of the circle.

Example:

Construct the pair of tangents to the circle of radius 3 cm from the point which is 7 cm away from its centre, and measure their lengths also.

Steps of Construction

Step 1: Draw a circle of radius 3 cm by taking O as the centre.

Step 2: Mark a point P outside the circle at a distance of 7 cm from the centre O. Join OP.

Step 3: Bisect the line segment OP, so that the perpendicular bisector of OP intersects it at the point M.

Step 4: Now draw another circle by taking M as centre and MO as radius, which intersects the given circle at two points’ i.e. T and Tꞌ.

Step 5: Now join PT and PTꞌ which are the required tangents and measure the length of the tangents.

The length of the tangents is PT = PTꞌ = 6.3 cm.

 

cbse class 10th constructions 

Share:

Read More

Class 10 Chapter 10 (Circles) class notes

 

CBSE Class 10 Maths Notes Chapter 10 Circles

 

Circle: A circle is a collection of all points in a plane which are at a constant distance from a fixed point.

Centre: The fixed point is called the centre.

Radius: The constant distance from the centre is called the radius.

Chord: A line segment joining any two points on a circle is called a chord.

Diameter: A chord passing through the centre of the circle is called diameter. It is the longest chord.

Tangent: When a line meets the circle at one point or two coincidings The line is known as points, a tangent.
The tangent to a circle is perpendicular to the radius through the point of contact.
⇒ OP ⊥ AB

The lengths of the two tangents from an external point to a circle are equal.
⇒ AP = PB

Length of Tangent Segment
PB and PA are normally called the lengths of tangents from outside point P.

Properties of Tangent to Circle

Theorem 1: Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: XY is a tangent at point P to the circle with centre O.
To prove: OP ⊥ XY
Construction: Take a point Q on XY other than P and join OQ
Proof: If point Q lies inside the circle, then XY will become a secant and not a tangent to the circle
OQ > OP

This happens with every point on the line XY except the point P. OP is the shortest of all the distances of the point O to the points of XY
OP ⊥ XY …[Shortest side is the perpendicular]

Theorem 2: A line drawn through the end point of a radius and perpendicular to it, is the tangent to the circle.
Given: A circle C(O, r) and a line APB is perpendicular to OP, where OP is the radius.
To prove: AB is tangent at P.
Construction: Take a point Q on the line AB, different from P and join OQ.
Proof: Since OP ⊥ AB
OP < OQ ⇒ OQ > OP

The point Q lies outside the circle.
Therefore, every point on AB, other than P, lies outside the circle.
This shows that AB meets the circle at point P.
Hence, AP is a tangent to the circle at P.

Theorem 3: Prove that the lengths of tangents drawn from an external point to a circle are equal
Given: PT and PS are tangents from an external point P to the circle with centre O.
To prove: PT = PS
Construction: Join O to P, T and S.

Proof: In ∆OTP and ∆OSP.
     OT = OS      …[radii of the same circle]
     OP = OP      …[common]
∠OTP = ∠OSP …[each 90°]
∆OTP = ∆OSP  …[R.H.S.]
     PT = PS       …[CPCT.]

Note: If two tangents are drawn to a circle from an external point, then:

• They subtend equal angles at the centre i.e., ∠1 = ∠2.
• They are equally inclined to the segment joining the centre to that point i.e., ∠3 = ∠4.
  ∠OAP = ∠OAQ
  

  

Number of Tangents from a Point on a Circle

1. There could be only one tangent at one point of contact.

2. Tangent could not be drawn from any point inside the circle. 3. There could be only two tangents to a circle from any point outside the circle.

The lengths of tangents drawn from an external point to a circle are equal.

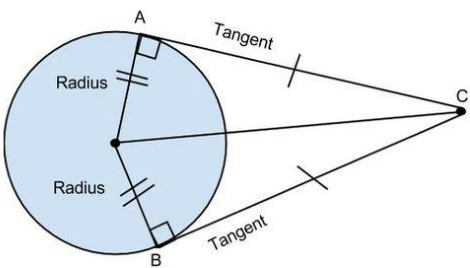
Here, two tangents are drawn from the external point C. As the tangent is perpendicular to the radius, it formed the right angle triangle. So ∆AOC and ∆BOC are congruent right angle triangle. Hence AC = BC.
Example

If two tangents PA and PB are drawn to a circle from a point P with centre O and OP is equal to the diameter of the circle then show that triangle APB is an equilateral triangle.

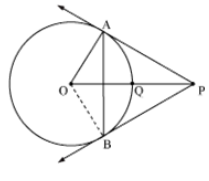
SolutionGiven, AP is a tangent to the circle. Therefore, OA ⊥ AP (Tangent is perpendicular to the radius through the point of contact) ∠OAP = 90° In ∆OAP,

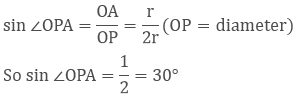
Likewise, we can prove that ∠OPB = 30°
Now, ∠APB = ∠OPA + ∠OPB = 30° + 30° = 60°
In ∆PAB, PA = PB (length of the tangents from the external point is equal)
∠PAB = ∠PBA (Angles opposite to equal sides are equal)
∠PAB + ∠PBA + ∠APB = 180° (Due to angle sum property)
∠PAB + ∠PBA = 180° - 60°
2∠PAB = 120
∠PAB = 60°
As ∠PAB = ∠PBA = ∠APB = 60°
Hence, PAB is an equilateral triangle.

Example
Find the length of AB in the given circle, which is the chord in the outer circle and tangent to the inner circle. The radius of the inner and outer circle is 6 cm and 10 cm respectively.

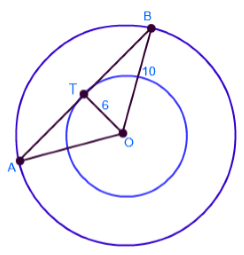
Solution :
Given :
Radius of the inner circle (r) = 6 cm
Radius of outer circle (R) = 10 cm
As the Point T which is the tangent point is the midpoint of the chord, AT = TB
As radius is perpendicular to the tangent,
So is a right angle triangle and we can use Pythagoras theorem.
OB² = OT² + TB²
TB² = OB² - OT²

= 10² - 6²

= 100 – 36

 TB² = 64

TB = 8 cm

AB = TB + AT

AB = 8 + 8 (AT = BT)

AB = 16 cm

cbse class 10th circles

Share:

Read More

Class 10 Chapter 9 (some applications on trigonometry) class notes

Notes on Some Applications of Trigonometry

Trigonometry can be used in many ways in the things around us like we can use it for calculating the height and distance of some objects without calculating them actually.

Heights and Distances

To find the height of an object or to find the distance of an object to the other we must know the meaning of some points -

Line of Sight

When we look at some object then the line made by our vision to the object is called the Line of Sight.

Horizontal Line

A horizontal line is a distance between the observer and the object.

Angle of Elevation

An angle of elevation is the angle made by the line of sight to the top of the object and the horizontal line. It is above the horizontal line i.e. the angle of elevation is made when we look up to the object.

Angle of Depression

An angle of depression is made when the observer needs to look down to see the object.The angle between the horizontal line and the line of sight is the angle of depression when the horizontal line is above the angle.

Some Solved Examples

To solve the problems related to the angle of elevation and angle of depression we must remember trigonometric ratios, trigonometric table and the trigonometric identities.

Example: 1

Find the height of the flagpole if the angle of elevation is 30° and the distance of flag from the observer is 15 m.

Solution:

Let x be the height of the flagpole.

Horizontal line is 15m.

Now, to calculate x, we need to take the trigonometric ratio which includes perpendicular and base.

Hence, the flagpole is 9 m.

Example: 2

A child was playing at the top of the hill. He had thrown a stone in the lake from the hill, the distance covered by the stone was 150 m and the angle of depression was 30°, then what is the height of the hill?

Solution:

Let the height of the hill be h.

The hypotenuse is 150 m and the angle of depression is 30°.

Hence the height of the hill is 75 m.

Example: 3

A person standing at point A is looking up at the angle of elevation of 45° to the aeroplane which is at the height of 100 m. As the airplane is going upwards, after some, the person was looking at the angle of elevation of 60°. Then what will be the increase in the height of the aeroplane from the ground at the angle of 60°?

Solution:

Given

∠CAB = 45°, ∠DAB = 60°

Distance of the aero plane from the ground = x + 100 m

In ∆ABC

AB = BC = 100 m

In ∆ABD

BD = BC + CD

100√3m = 100 + x

x = 100(√3 - 1) m

Hence, the increase in the height of the aero plane is100 (√3 -1) m.

Example: 4

A girl who is 1.2 m tall is watching a ballon moving in a horizontal line at a height of 88.2 m from the ground.The angle of elevation from her eyes is changed from 60° to 30°. Calculate the distance travelled by balloon.

Solution:

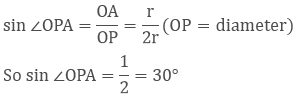
In ΔACE

In ΔBCG

CG = 87√3 m

Distance travelled by ballon = EG = CG - CE

87√3 - 29√3 = 58√3 m

cbse class 10th Heights and distances

Share:

Read More

Linear Equations in Two Variables Class notes

Basics Revisited

Equation

An equation is a statement that two mathematical expressions having one or more variables are equal.

Linear Equation

Equations in which the powers of all the variables involved are one are called linear equations. The degree of a linear equation is always one.

To know more about Linear Equation, visit here

General form of a Linear Equation in Two Variables

The general form of a linear equation in two variables is ax + by + c = 0, where a and b cannot be zero simultaneously.

Representing linear equations for a word problem

To represent a word problem as a linear equation

• Identify unknown quantities and denote them by variables.
• Represent the relationships between quantities in a mathematical form, replacing the unknowns with variables.

Solution of a Linear Equation in 2 variables

The solution of a linear equation in two variables is a pair of values, one for x and the other for y, which makes the two sides of the equation equal.
Eg: If 2x+y=4, then (0,4) is one of its solutions as it satisfies the equation. A linear equation in two variables has infinitely many solutions.

Geometrical Representation of a Linear Equation

Geometrically, a linear equation in two variables can be represented as a straight line.
2x – y + 1 = 0

⇒ y = 2x + 1

Graph of y = 2x+1

To know more about Linear Equation in Two Variables, visit here.

Plotting a Straight Line

The graph of a linear equation in two variables is a straight line. We plot the straight line as follows:

Any additional points plotted in this manner will lie on the same line.

Share:

Read More

Class 10 Chapter 8 (Introduction to Trigonometry) class notes

Notes on Introduction to Trigonometry

Trigonometry

To find the distances and heights we can use the mathematical techniques, which come under the Trigonometry. It shows the relationship between the sides and the angles of the triangle. Generally, it is used in the case of a right angle triangle.

Trigonometric Ratios

In a right angle triangle, the ratio of its side and the acute angles is the trigonometric ratios of the angles.

In this right angle triangle $\angle B={90}^{\circ }$. If we take $\angle A$ as acute angle then -

AB is the base, as the side adjacent to the acute angle.

BC is the perpendicular, as the side opposite to the acute angle.

Ac is the hypotenuse, as the side opposite to the right angle.

Trigonometric ratios with respect to ∠A

Ratio	Formula	Short form	Value
sin A		$\frac{P}{H}$	$\frac{BC}{AC}$
cos A		$\frac{B}{H}$	$\frac{AB}{AC}$
tan A		$\frac{P}{B}$	$\frac{BC}{AB}$
cosec A		$\frac{H}{P}$	$\frac{AC}{BC}$
sec A		$\frac{H}{B}$	$\frac{AC}{AB}$
cot A		$\frac{B}{P}$	$\frac{AB}{BC}$

Remark

• If we take ∠C as acute angle then BC will be base and AB will be perpendicular. Hypotenuse remains the same i.e. AC.So the ratios will be according to that only.
• If the angle is same then the value of the trigonometric ratios of the angles remain the same whether the length of the side increases or decreases.
• In a right angle triangle, the hypotenuse is the longest side so sin A or cos A will always be less than or equal to 1 and the value of sec A or cosec A will always be greater than or equal to 1.

Reciprocal Relation between Trigonometric Ratios

Cosec A, sec A, and cot A are the reciprocals of sin A, cos A, and tan A respectively.

Quotient Relation

Trigonometric Ratios of Some Specific Angles

Use of Trigonometric Ratios and Table in Solving Problems

Example

Find the lengths of the sides BC and AC in ∆ ABC, right-angled at B where AB = 25 cm and ∠ACB = 30°, using trigonometric ratios.

Solution

To find the length of the side BC, we need to choose the ratio having BC and the given side AB. As we can see that BC is the side adjacent to angle C and AB is the side opposite to angle C, therefore

tan 30°

BC = 25√3 cm

To find the length of the side AC, we consider

AC = 50 cm

Trigonometric Ratios of Complementary Angles

If the sum of two angles is 90° then, it is called Complementary Angles. In a right-angled triangle, one angle is 90°, so the sum of the other two angles is also 90° or they are complementary angles.so the trigonometric ratios of the complementary angles will be -

sin (90° – A) = cos A,

cos (90° – A) = sin A,

tan (90° – A) = cot A,

cot (90° – A) = tan A,

sec (90° – A) = cosec A,

cosec (90° – A) = sec A

Trigonometric Identities (Pythagoras Identity)

An equation is said to be a trigonometric identity if it contains trigonometric ratios of an angle and satisfies it for all values of the given trigonometric ratios.

In ∆PQR, right angled at Q, we can say that

PQ² + QR² = PR²

Divide each term by PR², we get

$\begin{array}{l}\frac{P{Q}^2}{P{R}^2}+\frac{Q{R}^2}{P{R}^2}=\frac{P{R}^2}{P{R}^2}\\ {\left(\frac{PQ}{PR}\right)}^2+{\left(\frac{QR}{PR}\right)}^2=1\\ {\sin }^{2}R+{\cos }^{2}R=1\end{array}$

Likewise other trigonometric identities can also be proved. So the identities are-

$\begin{array}{l}{\sin }^2\theta +{\cos }^2\theta =1\\ 1+{\tan }^2\theta ={\sec }^2\theta \\ {\cot }^2\theta +1=\cos e{c}^2\theta \end{array}$

How to solve the problems related to trigonometric ratios and identities?

Prove that

cbse class 10 introduction to trigonometry

Share:

Read More