Class 9 Chapter 10 (Circles) Notes

Notes of Chapter 10 Circles Class 9th Math

Terms Related to Circles

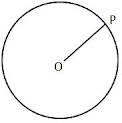
• The locus of a point which moves in a plane in such a manner that its distance from a given fixed point is always constant, is called a circle.
• The fixed point is called the centre and constant distance is called the radius of the circle.
  In the figure, ‘O’ is centre and OP = r is a radius. We denote it by C(O, r).

• A line segment, terminating (or having its end points) on the circle is called a chord. A chord, passing through the centre is called a diameter of the circle. 
• A line which intersects a circle in two distinct points is called a secant of the circle.
• A line intersecting the circle in exactly one point is called a tangent to the circle.

• In the figure, PQ is a chord, AB is a diameter, XY is a secant and ST is a tangent to the circle at C.

Note: 
(i) Diameter is the longest chord in a circle.
(ii) Diameter = 2 × Radius

• The length of the complete circle is called its circumference, whereas a piece of a circle between two points is called an arc.

Note: 
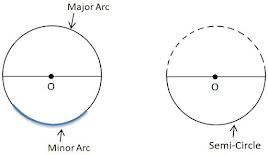
(i) A diameter of a circle divides it into two equal arcs, each of which is called a semicircle.
(ii) If the length of an arc is less than the semicircle, then it is a minor arc, otherwise, it is a major arc.

• The region consisting of all points lying on the circumference of a circle and inside it is called the interior of the circle.
• The region consisting of all points lying outside a circle is called the exterior of the circle.
• The region consisting of all points which are either on the circle or lie inside the circle is called the circular region.

• A chord of a circle divides it into two parts. Each part is called a segment. 
• The part containing the minor arc is called the minor segment, and the part containing the major arc is called the major segment. 

• A quadrilateral of which all the four vertices lie on a circle is called a cyclic quadrilateral. The four vertices A, B, C and D are said to be concyclic points.

Fundamentals of Circles

• Equal chords of a circle (or of congruent circles) subtend equal angles at the centre.
• If two chords of a circle subtend equal angles at the centre, then the chords are equal.
• The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
• The perpendicular from the centre of a circle to a chord bisects the chord.
• Equal chords of a circle are equidistant from the centre whereas the equidistant chords from the centre are equal.
• Chords corresponding to equal arcs are equal.
• Congruent arcs of a circle subtend equal angles at the centre.
• The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part.
• Angles in the same segment are equal, whereas the angle in a semicircle is a right angle.
• The sum of either pair of opposite angles of a cyclic quadrilateral is 180º.
• If the opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
• If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, then the four points are cyclic.

 

Theorems Related to Circles:

(1) Prove that If two arcs of circle are congruent,  then corresponding chords are equal.

Given: Arc PQ of a Circle C(O,r) and arc RS of another circle C(O′,r) such that PQ≅RS
To Prove:PQ = RS
Construction: Draw Line segment OP, OQ, O′R and O′S.

Proof:
Case-I When arc(PQ) and arc(RS) are minor Arcs
In triangle OPQ and O′RS, We have
OP = OQ = O′R = O′S = r                   [Equal radii of two circles]
∠POQ=∠RO′S                 arc(PQ)≅arc(RS)⇒m(arc(PQ))≅m(arc(RS))⇒∠POQ=∠RO′S
So by SAS Criterion of congruence, we have
ΔPOQ≅ΔRO′S
⇒PQ=RS
Case-II When arc(PQ) and arc(RS) are major arcs.
If arc(PQ), arc(RS) are major arcs, then arc(QP) and arc(SR) are Minor arcs.
So arc(PQ)≅arc(RS)
⇒ arc(QP)≅arc(SR)
⇒QP=SR
⇒PQ=RS
Hence, PQ≅RS⇒PQ=RS

(2) Prove that If two chords of a circle are equal, then their corresponding arcs are congruent.

Given: Equal chords, PQ of a circle C(O,r)  and RS of congruent circle C(O′,r)
To Prove:arc(PQ)≅arc(RS), where both arc(PQ) and arc(RS) are minor, major or semi-circular arcs.
Construction: If PQ,RS are not diameters, draw line segments OP, OQ, O′R and O′S.

Proof:
Case I: when arc(PQ) and arc(RS) are diameters
In this case, PQ and RS are semi circle of equal radii, hence they are congruent.
Case II: When arc(PQ) and arc(RS) are Minor arcs.
In triangles POQ and RO′S, we have
PQ=RS
OP=O′R=r and OQ=O′S=r
So by SSS-criterion of congruence, we have
ΔPOQ≅ΔRO′S
⇒            ∠POQ=∠RO′S
⇒           m(arc(PQ))=m(arc(RS))
⇒         arc(PQ)≅arc(RS)
Case III: When arc(PQ) and arc(RS) are major arcs
In this case, arc(QP) And arc(SR)will be minor arcs.
PQ=RS
⇒            QP=SR
⇒           m(arc(QP))=m(arc(SR))
⇒           360∘−m(arc(PQ))−360∘−m(arc(RS))
⇒           m(arc(PQ))−m(arc(RS))
⇒           arc(PQ)≅arc(RS)
Hence, in all the three cases, we have arc(PQ)≅arc(RS)

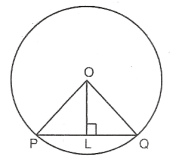
(3) Prove that The perpendicular from the centre of a circle to a chord bisects the chord.

Given: A Chord PQ of a circle C(O,r) and perpendicular OL to the chord PQ.
To Prove:LP=LQ
Construction: Join OP and OQ

Proof: In Triangles PLO and QLO, we have
OP=OQ=r                               [Radii of the same circle]
OL=OL                                       [Common]
And,      ∠OLP=∠OLQ     [Each equal to 90∘]
So, by RHS-criterion of congruence, we have
ΔPLO≅ΔQLO
⇒            PL=LQ

(4) Prove that The line segment joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.

Given: A Chord PQ OF a circle C(O,r) with mid-point M.
To Prove:OM⊥PQ
Construction: Join OP and OQ

Proof: In triangles OPM and OQM, we have
OP=OQ                                     [Radii of the same circle]
PM=MQ                                   [M is mid-point of PQ]
OM=OM
So, by SSC- criterion of congruence, we have
ΔOPM≅ΔOQM
⇒            ∠OMP=∠OMQ
But , ∠OMP+∠OMQ=180∘                                          [Linear pair]
⇒            ∠OMP+∠OMP=180∘  [∠OMP=∠OMQ]
⇒            2∠OMP=180∘
⇒            ∠OMP=90∘

(5) Prove that There is one and only circle passing through three given points.

Given: Three non-collinear points P,Q and R.
To Prove: There is one and only one circle passing through P,Q and R.
Construction: Join PQ and QR. Draw perpendicular bisectors AL and BM of PQ and RQ respectively. Since P,Q and R. are not collinear. Therefore, the perpendicular bisectors AL and BM are not parallel.
Let AL And BM intersect at O. Join OP,OQ and OR.

Proof: Since O lies on the perpendicular bisector of PQ.
Therefore,
OP=OQ
Again, O Lies on the perpendicular bisector of QR.
Therefore,
OQ=OR
Thus,     OP=OQ=OR=r    (say)
Taking O as the centre draw a circle of radius s. Clearly, C(O,s) passes through P, Q and R. This proves that there is a circle passing the points P,Q and R.
We shall now prove that this is the only circle passing through P,Q and R.
If possible, let there be another circle with centre O′ and radius r, passing through the points P,Q and R. Then, O′ will lie on the perpendicular bisectors AL of PQ and BM of QR.
Since two lines cannot intersect at more than one point, so O′ must coincide with O. Since OP=r, O′P=s and O and O′ coincide, we must have
r=s
⇒           C(O,r)=C(O′,s)
Hence, there is one and only one circle passing through three non-collinear points P,Q and R.

(6) Prove that If two circles intersect in two points, then the through the centre is perpendicular to the common chord.

Given: Two circles C(O,r) and C(O′,s) intersecting at points A and B.
To Prove:OO′ is perpendicular bisector of AB.
Construction: Draw line segments
OA,OB,O′A and O′B

Proof: In triangles OAO′ and OBO′,  we have
OA=OB=r
O′A=O′B=s
And,                OO′=OO′
So, by SSS-criterion of congruence, we have
ΔOAO≅ΔOBO′
⇒       ∠AOO′=∠BOO′
⇒       ∠AOM=∠BOM         [∠AOO′=∠AOM and ∠BOM=∠BOO′]
Let M be the point of intersection of AB and OO′
In triangles AOM and BOM, we have
OA=OB=r
⇒       ∠AOO′=∠BOO′
⇒       ∠AOM=∠BOM        [∠AOO′=∠AOM and ∠BOM=∠BOO′]
Let M be the point of intersection of AB and OO′
In triangles AOM and BOM, we have
OA=OB=r
∠AOM=∠BOM
And                 OM=OM
So, by SAS-criterion of congruence, we have
ΔAOM≅ΔBOM
⇒       AM=BM and ∠AMO=∠BOM
But,                             ∠AOM+∠BMO=180∘
2∠AOM=180∘
⇒       ∠AOM=90∘
Thus,                           AM=BM and ∠AOM=∠BMO=90∘
Hence, OO′ is the perpendicular bisector of AB.

(7) Prove that Equal chords of a circle subtend equal angle at the centre.

Given: Two Chord AB and CD of circle C(O,r) such that AB=CDand OL⊥AB and OM⊥CD
To Prove: Chord AB and CD are equidistant from the centre O i.e OL=OM.
Construction: Join OA and OC.

Proof: Since the perpendicular from the centre of a circle to a chord bisects the chord.
Therefore,
OL⊥AB⇒AL=12AB..........(i)
And,                OM⊥CD⇒CM=12CD..........(ii)
But,                 AB=CD
⇒       12AB=12CD
⇒       AL=CM                                [Using (i) and (ii) ]….......(iii)
Now, in right triangles OAL and OCM, we have
OA=OC                                           [Equal to radius of the circle]
AL=CM                                            [From equation (iii)]
And,                ∠ALO=∠CMO         [Each equal to 90∘]
So by RHS criterion of convergence, we have
ΔOAL≅ΔOCM
⇒       OL=OM
Hence, equal chord of a circle are equidistant from the centre.

(8) Prove that Chords of a circle which are equidistant from the centre are equal.

Given: Two Chords AB and CD of a circle C(O,r) which are equidistant from its centre i.e. OL=OM, where OL⊥AB and OM⊥CD.
To Prove: Chords are Equal i.e. AB=CD
Construction: Join OA and OC

Proof: Since the perpendicular from the centre of a circle to a chord bisects the chord.
Therefore,
OL⊥AB
⇒       AL=BL
⇒       AL=12AB
And,                            OM⊥CD
⇒       CM=DM
⇒       CM=12CD
In triangles OAL and OCM, we have
OA=OC                        [Each equal to radius of the given Circle]
∠OLA=∠OMC         [Each equal to 90∘]
And,                OL=OM                                            [Given]
So, by RHS, criterion of convergence, we have
ΔOAL≅ΔOCM
⇒       AL=CM
⇒       12AL=12AB
⇒       AB=CD
Hence, the chords of a circle which are equidistant from the centre are equal.

(9) Prove that Equal chords of a circle subtend equal angle at the centre.

Given: A circle C(O,r) and its two equal chords AB and CD.
To Prove:∠AOB=∠COD

Proof:In triangles AOB and COD, we have
AB=CD                                                [Given]
OA=OC                                     [Each equal to r]
OB=OD                                                [Each equal to r]
So, by SSC-criterion of Congruence, we have
ΔAOB≅ΔCOD
⇒       ∠AOB=∠COD

(15) Prove that If the angles subtended by two chords of a circle at the centre are equal, the chords are equal.

Given: Two Chord AB and CD of a circle C(O,r) such that ∠AOB=∠COD
To Prove: AB=CD

Proof: In triangles AOB and COD, we have
OA=OC                                     [Each equal to r]
∠AOB=∠COD         [Given]
OB=OD                                     [Each equal to r]
So, by SAS-criterion of congruence, we have
ΔAOB≅ΔCOD
⇒       AB=CD

(11) Prove that Of any two chords of a circle, the larger chord is nearer to the centre.

Given: Two Chord AB and CD of a circle with Centre O such that AB>CD
To Prove: Chord AB is nearer to the centre of the circle i.e. OL<OM, where OL and OM are perpendiculars from O to AB and CD respectively
Construction: Join OA and OC.

Proof: Since the perpendicular from the centre of a circle to a chord bisects the chord. Therefore,
OL⊥AB⇒AL=12AB
And,                OM⊥CD⇒CM=12CD
In right triangles OAL and OCM, we have
OA2=OL2+AL2
And,                OC2=OM2+CM2
⇒       OL2+AL2=OM2+CM2.. (i)  [OA=OC⇒OA2=OC2]
Now,                           AB>CD
⇒       12AB>12CD
⇒       AL>CM
⇒       AL2>CM2
⇒       OL2+AL2>OL2+CM2         [Adding OL2 on both sides]
⇒       OM2+CM2>OL2+CM2       [using equation (i)]
⇒       OM2>OL2
⇒       OM>OL
⇒       OL<OM
Hence, AB is nearer to the centre than CD.

(12) Prove that Of any two chords of a circle, the chord nearer to the centre is larger.

Given: Two Chord AB and CD of a circle C(O,r) such that OL<OM, where OL and OM are perpendiculars From O on AB and CD respectively.
To Prove:AB>CD
Construction: Join OA and OC.

Proof: Since the perpendicular From the Centre of a circle to a chord bisects the chord.
AL=12AB and CM=12CD
In right triangles OAL and OCM, we have
OA2=OL2+AL2 and, OC2=OM2+CM2
⇒       AL2=OA2−OL2....... (i)
And,                            CM2=OC2−OM2.......(ii)
Now,                           OL<OM
⇒       OL2<OM2
⇒       −OL2>−OM2
⇒       OA2−OL2>OA2−OM2         [adding OA2 on both sides]
⇒       OA2−OL2>OC2−OM2          [OA2=OC2]
⇒       AL2>CM2
⇒       AL>CM
⇒       2AL>2CM
⇒       AB>CD

(13) Prove that The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

Given: An arc PQ of a circle C(O,r) and a point R on the remaining part of the circle i.e. arc QP.
To Prove:∠POQ=2∠PRQ
Construction: join RO and produce it to a point M outside the circle.

Proof: We shall consider the following three different cases:
Case I: when arc(PQ) is a minor arc.
We know that an exterior angle of a triangle is equal to the sum of the interior oppsite angles.
In ΔPOQ, ∠POM is the exterior angle.
∠POM=∠OPR+∠ORP
⇒∠POM=∠ORP+∠ORP     [OP=OR=r, ∠OPR=∠ORP]⇒∠POM=2∠ORP.....................(i)
In ΔQOR, ∠QOM is the exterior angle.
∠QOM=∠OQR+∠ORQ
⇒∠QOM=∠OQP+∠ORQ   [OQ=OR=r, ∠ORQ=∠OQR]
⇒∠QOM=2∠ORQ................(ii)
Adding equation (i) and (ii), we get
∠POM+∠QOM=2∠ORP+2∠ORP
⇒∠POM+∠QOM=2(∠ORP+∠ORP)
⇒  ∠POM=2∠PRQ
Case II: when arc(PQ) is a semi-circle
We know that an exterior angle of a triangle is equal to the sum of the interior opposite angles.
In ΔPOQ, we have
∠POM=∠OPR+∠ORP
⇒∠POM=∠ORP+∠ORP     [OP=OR=r, ∠OPR=∠ORP]
⇒∠POM=2∠ORP.....................(iii)
In ΔQOR, We have
∠QOM=∠ORQ+∠OQR
⇒∠QOM=∠ORQ+∠ORQ   [OQ=OR=r, ∠ORQ=∠OQR]
⇒∠QOM=2∠ORQ................(iv)
Adding equations (iii) and (iv), we get
∠POM+∠QOM=2(∠ORP+∠ORQ)
∠POQ=2∠PRQ
Case III: When arc(PQ) is a major arc.
We know that an exterior angle of a triangle is equal to the sum of the interior opposite angles
In ΔPOR, we have
∠POM=∠ORP+∠ORP           [OP=OR=r, ∠OPR=∠ORP]
⇒∠POM=2∠ORP ...................(v)
In ΔQOR, we have
∠QOM=∠ORQ+∠OQR
⇒∠QOM=2∠ORQ ...................(vi)
Adding equations (v) and (vi), we get
∠POM+∠QOM=2(∠ORP+∠ORP)
⇒ Reflex ∠POQ=2∠PRQ

(14)Prove that Angles in the same segment of a circle are equal.

Given: A circle C(O,r), an arc PQ and two angles ∠PRQ and ∠PSQ in the same segment of  the circle.
To Prove:∠PRQ= ∠PSQ
Construction: Join OP and OQ

Proof: we know that the angle subtended by an arc at the centre is double the angle subtended by the arc at any point in the remaining part of the circle. So we have
∠POQ=2∠PRQ and ∠POQ=2∠PSQ
⇒2∠PRQ=2∠PSQ
⇒∠PRQ=∠PSQ
We have
Reflex ∠POQ=2∠PRQ and ∠POQ=2∠PSQ
⇒2∠PRQ=2∠PSQ
⇒∠PRQ=∠PSQ
Thus , in both the cases, we have
∠PRQ=∠PSQ

(15) Prove that The angle in a semi-circle is a right angle.

Given:PQ is a diameter of a circle C(O,r) and ∠PRQ is an angle in semi-circle.
To Prove:∠POQ=90∘

Proof: we know that the angle subtended by an arc of a circle at its centre is twice the angle formed by the same arc at a point on the circle. So, we have
∠POQ=∠PRQ
⇒180∘=2∠PRQ                                    [POQ is a straight line]
⇒∠PRQ=90∘

(16) Prove that The opposite angles of a cyclic quadrilateral are supplementary.

Given: A Cyclic quadrilateral ABCD
To Prove:∠A+∠C=180∘ and ∠B+∠D=180∘
Construction: Join AC and BD.

Proof: Consider side AB of quadrilateral ABCD as the Chord of the circle. Clearly, ∠ACB and ∠ADB are angles in the same segment determined by chord AB of the Circle.
∠ACB=∠ADB          ………….(i)
Now , consider the side BC of quadrilateral ABCD as the chord of the circle. We find that ∠BAC  and ∠BDC are angles in the same segment
∠BAC  = ∠BDC             [angles in the same segment are equal]..(ii)
Adding equation (i) and (ii), we get
⇒       ∠ACB+∠BAC=∠ADB+∠BDC
⇒       ∠ACB+∠BAC=∠ADC
⇒       ∠ABC+∠ACB+∠BAC=∠ABC+∠ADC
⇒       180∘=∠ABC+∠ADC         [sum of angle of triangle is 180∘ ]
⇒       ∠ABC+∠ADC=180∘
⇒       ∠B+∠D=180∘
But, ∠A+∠B+∠C+∠D=360∘
∠A+∠C=360∘−(∠B+∠D)
⇒∠A+∠C=360∘−180∘=180∘
Hence, ∠A+∠C=180∘ and ∠B+∠D=180∘
The converse of this theorem is also true as given below.

(17) Prove that If the sum of any pair of opposite angles of a quadrilateral is 180∘,then it is cyclic.

Given: A quadrilateral ABCD in which ∠B+∠D=180∘
To Prove: ABCD is acyclic quadrilateral.

Proof: If possible, Let ABCD be not cyclic quadrilateral. Draw a circle passing through three non-collinear points A, B and C. Suppose the circle meets AD or AD produced at D′. Join D′C.
Now, ABCD’ is a cyclic quadrilateral.
∠ABC+∠AD′C=180∘..............(i)
But, ∠B+∠D=180∘
i.e. ∠ABC+∠ADC=180∘..............(ii)
from (i) and (ii), we get
∠ABC+∠AD′C = ∠ABC+∠ADC
⇒       ∠AD′C = ∠ADC
⇒       An exterior angle of ΔCDD′ is equal to interior oppsite angle.
But, this is not possible, unless D′ coincides with D. Thus, the circle passing through A,B,C also passes through D.
Hence, ABCD is a cyclic Quadrilateral.

(18) Prove that If one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle.

Given: A Cyclic quadrilateral ABCD one of whose side AB is produced to E.
To Prove:∠CBE=∠ADC

Proof: Since ABCD is a quadrilateral and the sum of opposite pairs of angles in a cyclic quadrilateral is 180∘
∠ABC+∠ADC=180∘
But,     ∠ABC+∠CBE=180∘                                  [Liner Pairs]
∠ABC+∠ADC=∠ABC+∠CBE
⇒       ∠ADC=∠CBE
Or,                               ∠CBE=∠ADC

(19) Prove that The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.

Given: A Cyclic quadrilateral ABCD in which AP,BP,CR and DR are the bisectors of ∠A, ∠B, ∠C and ∠D respectively such that a quadrilateral PQRS is formed.
To Prove:PQRS is a cyclic quadrilateral.

Proof: In order to prove that PQRS is a cyclic quadrilateral, it is sufficient to show that
∠APB+∠CRD=180∘
Since the sum of the angles of a triangle is 180∘. Therefore, in triangles APB and CRD, we have
∠APB+∠PAB+∠PBA=180∘
And,                ∠CRD+∠RCD+∠RDC=180∘
⇒       ∠APB+12∠A+12∠B=180∘
And,                ∠CRD+12∠C+12∠D=180∘
⇒       ∠APB+12∠A+12∠B+∠CRD+12∠C+12∠D=180∘+180∘
∠APB+∠CRD+12{∠A+∠B+∠C+∠D}=360∘
∠APB+∠CRD+12{(∠A+∠C)+(∠B+∠D)}=360∘
∠APB+∠CRD+12(180∘+180∘)=360∘
∠APB+∠CRD=180∘
Hence, PQRS is a cyclic Quadrilateral.

(20) Prove that If two sides cyclic quadrilateral are parallel, then the remaining two sides are equal and the diagonals are also equal.

Given: A Cyclic quadrilateral ABCD in which AB∥DC.
To Prove: (i) AD=BC          (ii) AC=BD

Proof: In order to prove the desired results, it is sufficient to show that ΔADC≅ΔBCD. Since ABCD is cyclic Quadrilateral and sum of opposite pairs of angles in a cyclic Quadrilateral is 180∘
∠B+∠D=180∘........(i)
Since AB∥DC and BC is a transversal and sum of the interior angles on the same side of a transversal is 180∘
∠ABC+∠BCD=180∘
∠B+∠C=180∘...................(ii)
From (i) and (ii), we get
∠B+∠D=∠B+∠C
⇒       ∠C=∠D.................(iii)
Now, consider triangles ADC and BCD. In ΔADC and ΔBCD, we have
∠ADC=∠BCD           [From equation (iii)]
DC=DC                                  [Common]
And,                ∠DAC=∠CBD           [∠DAC and ∠CBD are angles in the segment of chord CD]
So, by AAS-criterion of congruence, we have
ΔADC≅ΔBCD
⇒       AD=BC and AC=BD

(21) Prove that If two opposite sides of a cyclic quadrilateral are equal, then the other two sides are parallel.

Given: A cyclic quadrilateral ABCD such that AD=BC.
To Prove: AB∥CD
Construction: Join BD.

Proof: We have,
AD=BC
⇒       DA⌢≅BC⌢
⇒       m(DA)⌢≅(BC)⌢
⇒       2∠2=2∠1
⇒       ∠2=∠1
But, these are alternate interior angles. Therefore, AB∥CD.

(22) Prove that An isosceles trapezium is cyclic.

Given: A trapezium ABCD in which AB∥DC and AD=BC
To Prove:ABCD is a cyclic trapezium.
Construction: Draw DE⊥AB and CF⊥AB.

Proof: In order to prove that ABCD is a cyclic trapezium, it is sufficient to show that ∠B+∠D=180∘.
In triangles DEA and CFB, we have
AD=BC                        [Given]
∠DEA=∠CFB           [Each equal to 90∘]
And,                DE=CF
So, by RHS-criterion of congruence, we have
ΔDEA≅ΔCFB
⇒       ∠A=∠B and ∠ADE=∠BCF
Now,               ∠ADE=∠BCF
⇒       90∘+∠ADE=90∘+∠BCF
⇒       ∠EDC+∠ADE=∠FCD+∠BCF
⇒       ∠ADC=∠BCD
⇒       ∠D=∠C
Thus,               ∠A=∠B and ∠C=∠D.
∠A+∠B+∠C+∠D=360∘
⇒       2∠B+2∠D=360∘
⇒       ∠B+∠D=180∘
Hence, ABCD is a cyclic quadrilateral.

...

Share:

Read More

Questions on polynomials Class 9 SET-3

Q1. Find the zeros of the polynomial

1. x² + 7x +  10
2. x² - 25

Q2. Factorize: 

1. 999² - 1
2. (10.2)³
3. 1002 × 998

Q3. Factorize:

1. x³ - 3x² - 9x - 5
2. x³ + 7x² - 21x - 27

Q4. Factorize:

1. \(3{x^2} + 27{y^2} + {z^2} - 18xy + 6\sqrt 3 yz - 2\sqrt 3 zx\)
2. 27x³ + 125y³
3. \(\dfrac{1}{{64}}{a^2} + {b^3} + 125{c^3} - \dfrac{{15}}{4}abc\)
4. \({x^3} - \dfrac{1}{{{x^3}}}\)
5. 8x³ - (2x - y)³
6. a⁶ - b⁶

Q5. Using factor theorem, show that (a - b) is the factor of a(b² - c²) + b(c² - a²) + c(a² - b²).

Q6. Factorize:

1. \(4\sqrt 3 {x^2} + 5x - 2\sqrt 3 \)
2. \(21{x^2} - 2x + \dfrac{1}{{21}}\)
3. 9(2a - b)² - 4(2a - b) - 13

Q7. Simplify and factorize (a + b + c)² - (a - b - c)² + 4b² - 4c² 

Q8. Factorize: (a² - b²)³ + (b² - c²)³ + (c² - a²)³

Q9. For what value of a is 2x³ + ax² + 11x + a + 3 exactly divisible by (2x - 1).

Q10. If x  - 2 is a factor of a polynomial f(x) = x⁵ - 3x⁴ - ax³ + 2ax + 4, then find the value of a.

Q11. Find the value of a and b so that x² - 4 is a factor of ax⁴ + 2x³ - 3x² + bx - 4

Q12. If x = 2 and x = 0 are zeroes of the polynomial 2x³ - 3x² + px + q, then find the value of p and q.

Q13. Find the value of a and b, so that x³ - ax² - 13x + b is exactly divisible by (x - 1) as well as (x + 3).

Q14. The polynomial x³ - mx² + 4x + 6 when divided by (x + 2) leaves remainder 14, find m.

Q15. If the polynomial ax³ + 3x² - 13 and 2x³  - 15x + a, when divided by (x - 2)  leave the same remainder. Find the value of a.

Q16. If both (x -  2) and \(\left( {x - \dfrac{1}{2}} \right)\)  are the factors of px² + 5x + r, show that p = r.

Q17. If f(x) = x⁴ - 2x³ + 3x² - ax + b is divided by x - 1 and x  + 1 the remainders are 5 and 19 respectively, then find a and b.

Q18. If A and B be the remainders when the polynomials x³ + 2x² - 5ax - 7 and x³ + ax² - 12x + 6 are divided by (x + 1) and (x - 2) respectively and 2A + B = 6, find the value of a.

Q19. Show that x + 1 and 2x - 3 are factors of 2x³ - 9x² + x + 12.

Q20. If sum of remainders obtained by dividing ax³ - 3ax² + 7x + 5 by (x + 1) is -36. find a.

....

Share:

Read More

Question on Polynomials Class 9 SET - 2

Questions on Polynomials Class 9 SET - 2

Q1. Factorize the following by splitting the middle term:

1. 3x² + 19x + 30
2. \(2\sqrt 2 {x^2} + 9x + 5\sqrt 2 \)
3. 3x² - 13x + 10

Q2. Factorize the following by factor theorem:

1. x³ + 9x² + 23x + 15
2. x³ + 6x² + 11x + 6

Q3. Factorize the following by using a suitable identity:

1. 4x² + 12xy + 9y²
2. 2a⁵ - 54a²
3. \(2\sqrt 2 {x^3} + 3\sqrt 3 {y^3}\)
4. x⁵ - x
5. x⁶ - y⁶
6. (a - b)³ + (b - c)³ + (c - a)³
7. x⁸ - y⁸
8. 27x³ - 135x² + 225x - 125

Q4. Evaluate the following by using a suitable identity:

1. 998³
2. (10.2)³
3. 998² - 4
4. 999² - 1
5. (-25)³ + 10³ + 15³
6. 10.2 × 9.8

Q5. If 5 is a zero of x³ + 5x² + 2x + 8, find k.

Q6. If (x - 2) is a zero of x³ - 4x² + kx - 8, find k.

Q7. If (x - 2) and (x + 3) are factors of x³ + ax² + bx - 30, find a and b.

Q8. If x + y + z = 8 and xy + yz + zx = 20, find the value of x³ + y³ + z³ - 3xyz.

Q9. If a + b + c = 9 and a² + b² + c² = 35, find the value of a³ + b³ + c³ - 3abc.

Q10. Find the value of (2.7)³ - (1.6)³ - (1.1)³ using a suitable identity.

Q11. Factorize the following by using a suitable identity:

1. a³ + b³ - 8c³ +6abc
2. \({\left( {\dfrac{a}{b}} \right)^3} + {\left( {\dfrac{b}{c}} \right)^3} + {\left( {\dfrac{c}{a}} \right)^3} - 3\)
3. 8x³ - 27y³ + 125z³ + 90xyz

Q12. Find the value of a³ + 8b³, if a + 2b = 10 and ab = 15.

Q13. Find the value of a³ + 27b³, if a - 3b = - 6 and ab = - 10.

Q14. find the value of m and n, if y² -1 is a factor of y⁴ + my³ + 2y² - 3y + n.

Q15. (x + 2) is a factor of mx³ + nx² + x - 6. it leaves the remainder 4 when divided by (x - 2). find m and n. 

Q16. The polynomials kx³ + 3x² - 3 and 2x³ - 5x + k leave the same remainder when divided by (x - 4). Find k.

Q17. Factorize: \({x^2} + \dfrac{1}{{{x^2}}} - 2\).

QQ18. If ab + bc + ca = 10 and a² + b² + c² = 44. find a³ + b³ + c³ - 3abc.

Q19. Show that x - 2 is a factor p(x) = x³ - 12x² + 44x - 48.

Q20. Factorize: x³ - 2x² - 5x + 6.

Q21. If x + p is a factor of p(x) = x⁵ - p²x³ + 44x - 40. Find p.

Q22. Factorize:

1. \({a^2} + \dfrac{1}{{{a^2}}} + 2\)
2. 3(x + 2)² + 17(x + 2) + 10
3. 4x² - 9y² + 20x + 25

...

Share:

Read More

Questions on Polynomials class 9 SET -1

Extra Questions on Polynomials Class 9

Q1. Find the remainder when \({y^3} + {y^2} - 2y + 5\) is divided by y - 5.

Q2. Determine the remainder when p(x) = \({x^3} + 3{x^2} - 6x + 15\) is divided by x - 2.

Q3.  When \(f(x) = {x^4} - 2{x^3} + 3b{x^2} - ax\) is divided by x+1 and x - 1, we get  remainder as 19 and 5 respectively. Find the remainder if f(x) is divided by x - 3.

Q4.  What must be subtracted from \(4{x^4} - 2{x^3} - 6{x^2} + x - 5\) so that the result is exactly divisible by \(2{x^2} + 3x - 2\) ?

Q5.  If (x + 1) and (x - 1) both are factors of \(a{x^3} + {x^2} - 2x + b\), find a and b.

Q6.  Factorize each of the following expressions:

1. \(48{x^3} - 36{x^2}\)
2. \(5{x^2} - 15xy\)
3. \(15{x^3}{y^2}z - 25x{y^2}{z^2}\)

Q7. Factorize:

1. \(2{x^2}(x + y) - 3(x + y)\)
2. \(5xy(5x + y) - 5y(5x + y)\)
3. \(x({x^2} + {y^2} - {z^2}) + y({x^2} + {y^2} - {z^2}) + z({x^2} + {y^2} - {z^2})\)
4. \(ab({a^2} + {b^2} - {c^2}) + bc({a^2} + {b^2} - {c^2}) + ca({a^2} + {b^2} - {c^2})\)

Q8. Factorize each of the following expressions:

1. \(25{x^2}{y^2} - 20x{y^2}z + 4{y^2}{z^2}\)
2. \(4{x^2} - 4\sqrt 7 x + 7\)
3. \(\dfrac{{{a^2}}}{{{b^2}}} + 2 + \dfrac{{{b^2}}}{{{a^2}}}\)
4. \(4{a^2} + 12ab + 9{b^2} - 8a - 12b\)

Q9. Factorize each of the following:

1. \(25{x^2} - 36{y^2}\)
2. \(2ab - {a^2} - {b^2} + 1\)
3. \(36{a^2} - 12a + 1 - 25{b^2}\)
4. \({a^4} - 81{b^4}\)
5. \({a^{12}}{b^4} - {a^4}{b^{12}}\)
6. \(4{x^2} - 9{y^2} - 2x - 3y\)

Q10. Factorize by completing the square.

1. \({a^4} + {a^2} + 1\)
2. \({y^4} + 5{y^2} + 9\)
3. \({x^4} + 4\)
4. \({x^4} + 4{x^2} + 3\)

Q11. Factorize by completing the square.

1. \({a^3} - 27\)
2. \(1 - 27{x^3}\)
3. \(8{x^3} - {(2x - 3y)^3}\)
4. \({a^8} - {a^2}{b^6}\)
5. \({a^3} - 5\sqrt 5 {b^3}\)

Q12. Factorize the following:

1. \(16{p^3}{q^2} + 54{r^3}\)
2. \(\dfrac{{{a^3}}}{8} + 8{b^3}\)
3. \(2\sqrt 2 {a^3} + 3\sqrt 3 {b^3}\)
4. \(8{a^4}b + \dfrac{1}{{125}}a{b^4}\)
5. \({a^7} - 64a\)

Q13.Q13. Factorize:

1. \({x^3} + 9{x^2} + 27x + 27\)
2. \({x^3} - 9{x^2}y + 27x{y^2} - 27{y^3}\)

Q14. Using identities, find the value of

1. 101²
2. 98²
3. (0.98)²
4. 101 × 99
5. 190 × 190 - 10 × 10

Q15. Expand using suitable identity

1. (x + 5y + 6z)²
2. (2a - 3b + 4c)²
3. ( - a + 6b + 5c)²
4. (- p + 4q - 3r)²

Q16. Expand using suitable identity

1. (2x + 5y)³
2. (5p - 3q)³
3. (- a + 2b)³

Q17. Evaluate using identities

1. 102³
2. 99³

Q18. Simplify : 

1. (2a + b)³ + (2a - b)³
2. (4x + 5y)³ - (4x - 5y)³

Q19. Factorize:

1. 30x³y + 24x²y² - 6xy
2. 5x(a - b) + 6y(a - b)

Q20. Factorize:

1. 9x² - y²
2. (3 - x)² - 36x²
3. (2x - 3y)² - (3x + 4y)²
4. 16x⁴ - y⁴

.....

Share:

Read More

Class 9 Chapter 9 (Areas of parallelogram and triangles) Notes

Notes of Chapter 9 Area of Parallelograms and Triangles

Topics in the Chapter

• Area of Plane Figures
• Fundamentals
• Theorems

Areas of Plane Figures

• Two congruent figures have equal areas.
• A diagonal of a parallelogram divides it into two triangles of equal area.
• Parallelograms on the same base (or equal base) and between the same parallels are equal in area.
• Triangles on the same base (or equal bases) and between the same parallels are equal in area.
• Area of a parallelogram = base × height.
• Area of a triangle = 1/2 ×base × height
• A median of a triangle divides it into two triangles of equal area.
• Diagonals of a parallelogram divides it into four triangles of equal area.

Fundamentals

• Two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base. 

Examples:

 

 

• Area of triangle is half the product of its base (or any side) and the corresponding altitude (or height).
• Two triangles with same base (or equal bases) and equal areas will have equal corresponding altitudes.
• A median of a triangle divides it into two triangles of equal areas. 

Theorems:

(1) Prove that a diagonal of a parallelogram divides it into two triangles of equal area.

Given:  A parallelogram ABCD in which BD is one of the diagonals.

To prove:   

Proof: Since two congruent geometrical figures have equal area. Therefore, in order to prove that it is sufficient to show that

ΔABD ≅ ΔCDB

In Δs ABD and CDB, we have

AB = CD

AD = CB

And, BD = DB

So, by SSS criterion of congruence, we have

ΔABD ≅ ΔCDB

Hence, ar(ΔABD) = ar(ΔCDB)

(2) Prove that parallelograms on the same base and between the same parallels are equal in area.

Given: Two parallelograms ABCD and ABEF, which have the same base AB and which are between the same parallel lines AB and FC.

To prove: ar(||gm ABCD) = ar(||gm ABCD)

Proof: In Δs ADF and BCE, we have

AD = BC

AF = BE

And, ∠DAF = ∠CBE         [ ⸪ AD ∥ BC and AF ∥ BE]

So, by SAS criterion of congruence, we have

ΔADF ≅ ΔBCE

ar(ΔADF) = ar(ΔBCE)   …..(i)

Now, ar(||gm ABCD) = ar(square ABED) + ar(ΔBCE)

ar(||gm ABCD) = ar(square ABED) + ar(ΔADF)    [Using(i)]

ar(||gm ABCD) = ar(||gm ABEF)

Hence, ar(||gm ABCD) = ar(||gm ABEF)

(3) Prove that the area of a parallelogram is the product of its base and the corresponding altitude.

Given: A parallelogram ABCD in which AB is the base and AL the corresponding altitude.

To prove: ar(parallelogram ABCD) = A B × AL

Construction: Complete the rectangle ALMB by drawing BM⊥CD.

Proof: Since ar(parallelogram ABCD) and rectangle ALMB are on the same base and between the same parallels.

ar(parallelogram ABCD)

= ar(rect.ALMB)

=AB × AL    [By rect. Area axiom area of a rectangle = Base \(\times\) Height]

Hence, ar(parallelogram ABCD) = AB×AL

(4) Prove that parallelograms on equal bases and between the same parallels are equal in area.

Given: Two parallelograms ABCD and PQRS with equal bases AB and PQ and between the same parallels AQ and DR.

To prove: ar(parallelogram ABCD) = ar(parallelogram PQRS)

Construction: Draw AL ⊥ DR and PM ⊥ DR

Proof: Since AB ⊥ DR, AL ⊥ DR and PM ⊥ DR

AL = PM

Now, ar(parallelogram ABCD) = AB × AL

ar(parallelogram ABCD) = PQ × PM  [AB = PQ and AL = PM]

ar(parallelogram ABCD) = ar(parallelogram PQRS)

(5) Prove that triangles on the same bases and between the same parallels are equal in area.

Proof: We have,

BD∥CA

And, BC∥DA

sq.BCAD is a parallelogram.

Similarly, sq.BCQP is a parallelogram.

Now, parallelograms ECQP and BCAD are on the same base BC, and between the same parallels.

ar(parallelogram BCQP) = ar(parallelogram BCAD)    ….(i)

We know that the diagonals of a parallelogram divides it into two triangles of equal area.

ar(ΔPBC) = \(\dfrac{1}{2}\)ar(parallelogram BCQP)   …..(ii)

And, ar(ΔABC) = \(\dfrac{1}{2}\)ar(parallelogram BCAQ)  ....(iii)

Now, ar(parallelogram BCQP) = ar(parallelogram BCAD) [ From (i)]

\(\dfrac{1}{2}\)ar(parallelogram BCQP) = \(\dfrac{1}{2}\)ar(parallelogram BCAD)

ar(ΔABC) = ar(ΔPBC)    [From (ii) and (iii)]

Hence, ar(ΔABC) = ar(ΔPBC)

(6) Prove that the area of a triangle is half the product of any of its sides and the corresponding altitude.

Given: A ΔABC in which AL is the altitude to the side BC.

To prove:

Construction: Through C and A draw CD ∥ BA and AD ∥ BC respectively, intersecting each other at D.

Proof: We have,

BA∥CD and AD ∥ BC

So, BCDA is a parallelogram.

Since AC is a diagonal of parallelogram BCDA.

[BC is the base and AL is the corresponding altitude of parallelogram BCDA]

(7) Prove that if a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is equal to the half of the parallelogram.

Given: A ΔABC and a parallelogram BCDE on the same base BC and between the same parallel BC and AD.

To prove: ar(ΔABC) = \(\dfrac{1}{2}\)ar(||gm BCDE)

Construction: Draw AL ⊥ BC and DM ⊥ BC, meeting BC produced in M.

Proof: Since A, E and D are collinear and BC ∥ AD

AL = DM    …..(i)

Now,

ar(ΔABC) = \(\dfrac{1}{2}\)(BC × AL)

ar(ΔABC) = \(\dfrac{1}{2}\)(BC × DM)   [AL = DM (from (i)]

ar(ΔABC) = \(\dfrac{1}{2}\)ar(parallelogram BCDE)

 

(8) Prove that the area of a trapezium is half the product of its height and the sum of parallel sides.

Given: A trapezium ABCD in which AB ∥ DC; AB = a, DC = b and AL = CM = h, where AL⊥DC and CM ⊥ AB.

To prove: ar(trap. ABCD) = \(\dfrac{1}{2}\)h × (a + b)

Construction: Join AC

Proof: We have,

ar(trap. ABCD) = ar(ΔABC) + ar(ΔACD)

ar(trap. ABCD) = \(\dfrac{1}{2}\)(AB × CM) + \(\dfrac{1}{2}\)(DC × AL)

ar(trap. ABCD) = \(\dfrac{1}{2}\)ah + \(\dfrac{1}{2}\)bh  [AB = a and DC = b]

ar(trap. ABCD) = \(\dfrac{1}{2}\)h×(a+b)

(9) Prove that triangles having equal areas and having one side of one of the triangles, equal to one side of the other, have their corresponding altitudes equal.

Given: Two triangles ABC and PQR such that:

ar(ΔABC) = ar(ΔPQR)

AB = PQ

CN and RT are the altitudes corresponding to AB and PQ respectively of the two triangles.

To prove: CN = RT

Proof: In ΔABC, CN is the altitude corresponding to side AB.

ar(ΔABC) = \(\dfrac{1}{2}\)(AB × CN)    ….(i)

Similarly, we have,

ar(ΔPQR) = \(\dfrac{1}{2}\)(PQ × RT)   …..(ii)

Now, ar(ΔABC) = ar(ΔPQR)

\(\dfrac{1}{2}\)(AB × CN) = \(\dfrac{1}{2}\)(PQ × RT)

(AB × CN) = (PQ × RT)

(PQ × CN) = (PQ × RT)    [ AB = PQ (Given)]

CN = RT

(10) Prove that if each diagonal of a quadrilateral separates it into two triangles of equal area, then the quadrilateral is a parallelogram.

Given: A quadrilateral ABCD such that its diagonals AC and BD are such that

ar(ΔABD) = ar(ΔCDB) and ar(ΔABC) = ar(ΔACD)

To prove: Quadrilateral ABCD is a parallelogram.

Proof: Since diagonal AC of the quadrilateral ABCD separates it into two triangles of equal area. Therefore,

ar(ΔABC) = ar(ΔACD)    …..(i)

But, ar(ΔABC) + ar(ΔACD) = ar(ABCD)

2ar(ΔABC) = ar(ABCD)    [Using (i)]

ar(ΔABC) = \(\dfrac{1}{2}\)ar(ABCD) ….(ii)

Since diagonal BD of the quadrilateral ABCD separates it into triangles of equal area.

ar(ΔABD) = ar(ΔBCD)   ….(iii)

But, ar(ΔABD) + ar(ΔBCD) = ar(ABCD)

2ar(ΔABD) = ar(ABCD)    [Using(iii)]

ar(ΔABD) = \(\dfrac{1}{2}\)ar(ABCD)   …..(iv)

From (ii) and (iv), we get

ar(ΔABC) = ar(ΔABD)

Since Δs ABC and ABD are on the same base AB. Therefore they must have equal corresponding altitudes.

i.e. Altitude from C of ΔABC = Altitude from D of ΔABD

DC∥AB

Similarly, AD∥BC

Hence, quadrilateral ABCD is a parallelogram.

(11) Prove that the area of a rhombus is half the product of the lengths of its diagonals.

Given: A rhombus ABCD whose diagonals AC and BD intersect at O.

To prove: ar(rhombus ABCD) = \(\dfrac{1}{2}\)(AC×BD)

Proof: Since the diagonals of a rhombus intersect at right angles. Therefore,

OB ⊥ AC and OD ⊥ AC

ar(rhombus) = ar(ΔABC) + ar(ΔADC)

ar(rhombus) = \(\dfrac{1}{2}\)(AC × BO) + \(\dfrac{1}{2}\)(AC × DO)

ar(rhombus) = \(\dfrac{1}{2}\)(AC × (BO + DO))

ar(rhombus) =\(\dfrac{1}{2}\)(AC×BD)

(12) Prove that diagonals of a parallelogram divide it into four triangles of equal area.

Given: A parallelogram ABCD. The diagonals AC and BD intersect at O.

To prove: ar(ΔOAB) = ar(ΔOBC) = ar(ΔOCD) = ar(ΔAOD)

Proof: Since the diagonals of a parallelogram bisect each other at the point of intersection.

OA = OC and OB = OD

Also, the median of a triangle divides it into two equal parts.

Now, in ΔABC, BO is the median.

ar(ΔOAB) = ar(ΔOBC)  ….(i)

In ΔBCD, CO is the median

ar(ΔOBC) = ar(ΔOCD)    …..(ii)

In ΔACD, DO is the median

ar(ΔOCD) = ar(ΔAOD)   ….(iii)

From (i), (ii) and (iii), we get

ar(ΔOAB) = ar(ΔOBC) = ar(ΔOCD) = ar(ΔAOD)

(13) Prove that if the diagonals AC and BD of a quadrilateral ABCD, intersect at O and separate the quadrilateral into four triangles of equal area, then the quadrilateral ABCD is parallelogram.

Given: A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that

ar(ΔOAB) = ar(ΔOBC) = ar(ΔOCD) = ar(ΔAOD)

To prove: Quadrilateral ABCD is a parallelogram.

Proof: We have,

ar(ΔAOD) = ar(ΔBOC)

ar(ΔAOD) + ar(ΔAOB) = ar(ΔBOC) + ar(ΔAOB)

ar(ΔABD) = ar(ΔABC)

Thus, Δs ABD and ABC have the same base AB and have equal areas. So, their corresponding altitudes must be equal.

Altitude from ΔABD Altitude from C of ΔABC

DC ∥ AB

Similarly, we have, AD ∥ BC.

Hence, quadrilateral ABCD is a parallelogram.

(14) Prove that a median of a triangle divides it into two triangles of equal area.

Given: A ΔABC in which AD is the median.

To prove: ar(ΔABD) = ar(ΔADC)

Construction: Draw AL ⊥ BC.

Proof: Since AD is the median of ΔABC. Therefore, D is the mid point of BC.

BD = DC

BD × AL = DC × AL  [ Multiplying both sides by AL]

\(\dfrac{1}{2}\)(BD × AL) = \(\dfrac{1}{2}\)(DC × AL)

ar(ΔABD) = ar(ΔADC)

ALITER, Since Δs ABD and ADC have equal bases and the same altitude AL.

ar(ΔABD) = ar(ΔADC)

Share:

Read More