Class 9 Chapter 3 (Coordinate Geometry) Class Notes

 

Coordinate Geometry

Cartesian System

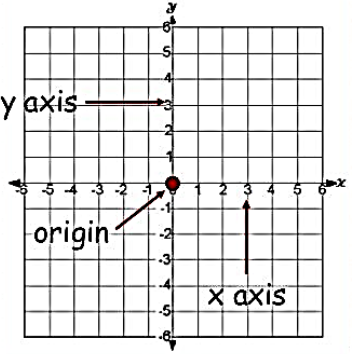
If we take two number lines, one horizontal and one vertical, and then combine them in such a way that they intersect each other at their zeroes, and then they form a Cartesian Plane.

• The horizontal line is known as the x-axis and the vertical line is known as the y-axis.

• The point where these two lines intersects each other is called the origin. It is represented as ‘O’.

• OX and OY are the positive directions as the positive numbers lie in the right and upward direction.

• Similarly, the left and the downward directions are the negative directions as all the negative numbers lie there.

Quadrants of the Cartesian Plane

The Cartesian plane is dividing into four quadrants named as Quadrant I, II, III, and IV anticlockwise from OX.

 

Coordinates of a Point

To write the coordinates of a point we need to follow these rules-

• The x - coordinate of a point is marked by drawing perpendicular from the y-axis measured a length of the x-axis .It is also called the Abscissa.

• The y - coordinate of a point is marked by drawing a perpendicular from the x-axis measured a length of the y-axis .It is also called the Ordinate.

• While writing the coordinates of a point in the coordinate plane, the x - coordinate comes first, and then the y - coordinate. We write the coordinates in brackets.

In the above figure, OB = CA = x coordinate (Abscissa), and CO = AB = y coordinate (Ordinate).

We write the coordinate as (x, y).

Remark: As the origin O has zero distance from the x-axis and the y-axis so its abscissa and ordinate are zero. Hence the coordinate of the origin is (0, 0).

The relationship between the signs of the coordinates of a point and the quadrant of a point in which it lies.

Quadrant	Coordinate	Sign in the quadrant
I	(+, +)	1st quadrant is enclosed by the positive x-axis and the positive y-axis.
II	(-, +)	2nd quadrant is enclosed by the negative x-axis and the positive y-axis.
III	(-, -)	3rd quadrant is enclosed by the negative x-axis and the negative y-axis.
IV	(+, -)	4th quadrant is enclosed by the positive x-axis and the negative y-axis

Plotting a Point in the Plane if its Coordinates are Given

Steps to plot the point (2, 3) on the Cartesian plane -

• First of all, we need to draw the Cartesian plane by drawing the coordinate axes with 1 unit = 1 cm.

• To mark the x coordinates, starting from 0 moves towards the positive x-axis and count to 2.

• To mark the y coordinate, starting from 2 moves upwards in the positive direction and count to 3.

• Now this point is the coordinate (2, 3)

Likewise, we can plot all the other points, like (-3, 1) and (-1.5,-2.5) in the right site figure.

Is the coordinates (x, y) = (y, x)?

Let x = (-4) and y = (-2)

So (x, y) = (- 4, – 2)

(y, x) = (- 2, - 4)

Let’s mark these coordinates on the Cartesian plane.

You can see that the positions of both the points are different in the Cartesian plane. So,

If x ≠ y, then (x, y) ≠ (y, x), and (x, y) = (y, x), if x = y.

 

 

Example: Write the coordinates of the points marked on the axes.From the figure,
(i) The coordinates of point A are (4, 0).
(ii) The coordinates of point B are (0, 3).
(iii) The coordinates of point C are (-5, 0).
(iv) The coordinates of point D are (0, -4).
(v) The coordinates of point E are (2/3, 0).

 

 

 

 

Example:

Plot the points (6, 4), (- 6,- 4), (- 6, 4) and (6,- 4) on the Cartesian plane.

Solution:

As you can see in (6, 4) both the numbers are positive so it will come in the first quadrant.

For x coordinate, we will move towards the right and count to 6.

Then from that point go upward and count to 4.

Mark that point as the coordinate (6, 4).

 Similarly, we can plot all the other three points.

Share: